One of the fundamental flaws with process improvement programs is the assumption that all aspects of a business environment are determinant and predictable to a high degree of precision. Certainly some business systems and functions fall into this highly predictable category and fit well into the various quality programs we have seen.
What happens, though, when you try to apply Six Sigma tools to a process or function that is indeterminate? The answer is that incorrect conclusions can be drawn. To be clear, predictions that have a higher precision than the evaluated process or function is capable of, need to be viewed with suspicion. Examples of indeterminate systems are the weather and search engine impressions that a keyword receives on a periodic basis.
The internet, like the weather is an indeterminate system. With indeterminate systems, macro (low precision) predictions can be made reliability (hot in summer, cold in winter) because at the macro level indeterminate systems demonstrate repeatable cyclic behavior. At the micro level, though, this repeatable cyclic behavior becomes less consistent and less reliable. For more on this read the work of Edward Lorenz regarding chaos and weather prediction.
Getting back to the internet, economic systems are indeterminate. This does not mean that Six Sigma tools cannot be applied to indeterminate systems like internet search engine key word impressions. It is instead a matter of using the right tool for the job. In indeterminate systems, since you cannot control or adequately predict all of the variables in the system being worked on, a Six Sigma project team will focus on less precise factors (macro). This means statistical inferences that have much higher standard deviation parameters and may even defy statistical evaluation altogether.
With indeterminate systems, the Six Sigma team will be trying to reduce uncertainties surrounding the system and determine the boundaries associated with these uncertainties. We have to realize that we cannot increase the precision of an indeterminate system beyond the system’s natural state. We can, though, control the precision of how we react to the system’s behavior.
With internet impressions, you may not be able to predict search engine behavior very far into the future, but you can calibrate how you will act to take advantage of what you see. For example, you can build a website that is robust enough to deal with the uncertainty of web searches on the internet. You can also take more frequent measurements of key word impressions and use pay per click tools to react to the impression “terrain”.
Basically, what I am saying is that with determinate systems, Six Sigma teams can work directly on the process to reduce variation and improve performance. With indeterminate systems, the team must work with the uncertainty that exists outside the process to improve performance.
Tag Archives: standard deviation
Variation Analysis
Variation
First, remember that not all variation is bad. Planned variation, like that in an experiment, is a process improvement strategy. Unplanned variation, on the other hand, is nearly always bad.
Two types of variation concern a process improvement team. These are common cause and special cause variation. All processes will have common cause variation. This variation is a normal part of the process (noise). It demonstrates the process’ true capability. Special cause variation on the other hand is not normal to the process. It is the result of exceptions in the process’ environment or inputs.
In a process improvement project, the first step is to eliminate special causes of variation and the second is to reduce common cause variation. Eliminating special causes of variation brings the process into a state of control and exposes the sources of common cause variation.
Common Cause Variation
Common cause variation is intrinsic to the process. It is random in nature and has predictable magnitude. Process noise is another name for it. An example would be the variation in your travel time to work everyday, with the absence of accidental, mechanical, or weather-related delays. When a process is expressing only common cause variation, its true capability for satisfying the customer is discernable. In this circumstance, the process is in control. Note that being in statistical control does not mean that the process is meeting customer expectations. The process could be precisely inaccurate.
Continuing with the travel time example above, one source of common cause variation would be the typical ebb and flow of traffic on your route to work. Remember from the Define Phase that Y = f(x1 + x2 + … + xn). In the example, Y is the travel time and each x is an input that contributes to travel time; examples of x might include time of day or the day of week.
Special Cause variation
Special cause variation is the variation that is not a normal part of process noise. When special cause variation is present, it means that something about the process has changed. Special cause variation has a specific, identifiable cause. An example of special cause variation would be the effect of an accident or a mechanical problem on your travel time to work.
Special cause variation is the first focus of process improvement efforts. When special cause variation exists, it is not possible to determine the process’ true capability to satisfy the customer. This is due to the effect that special cause variation has on inferences about central tendency (average) and standard deviation (spread in the data).
Statisticians have developed specific control chart tests that describe the presence, timing, and behavior of various special cause variation components. These tests point out the impact of variation on the process’ output.
Standard Deviation
Process improvement teams use statistics to describe datasets and to make predictions about the future based on past events. Two important data characteristics used in descriptive statistics are standard deviation and central tendency (average, mean).
Standard deviation is the measure of the dispersion or spread of a dataset. It is one of the more important parameters in statistical analysis. There are different ways to measure this parameter. Some of these are:
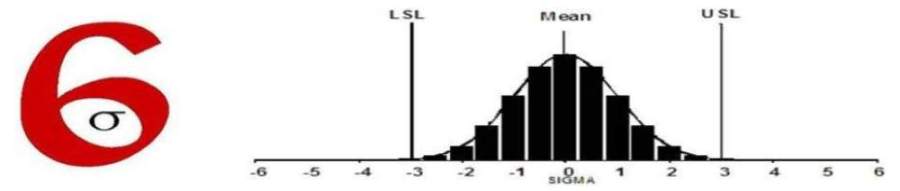
Range: This is the difference between the largest and the smallest observation in a dataset. The range has a variety of uses, including the calculation of control chart control limits. In a normally distributed dataset, with no special cause variation, the range divided by six is an estimate of standard deviation. This is because 99 percent of the observations in a normally distributed dataset, with no special cause variation, fall within ±3 standard deviations from the mean. If the presence of special cause variation is unknown, divide the range by four. Th
Statistics and Lean Six Sigma Process Improvement
Process improvement strategies use two applications of statistics. These are descriptive and inferential statistics. Descriptive statistics describe the basic characteristics of a data set. It uses the data’s mean, median, mode, and standard deviation to create a picture of the behavior of the data.
Inferential statistics uses descriptive statistics to infer qualities on a population, based on a sample from that population. This involves making predictions. Examples of this are voter exit poling, sporting odds, and predicting customer behavior.
Statistics are an important part of process improvement. Even so, statistical calculations do not solve problems. Business acumen and non-statistical tools are partners with statistical calculations in establishing root causes and in developing solutions. As important as some sources tend to make statistical tools, improvement projects rarely fail because of math problems. Instead, they fail due to a lack of honesty, management support, or a lack of business acumen. The best screwdriver in the world will still make a poor pry bar.